The historical significance of thermal light in quantum optics is without question: Planck argued the quantisation of light from black-body radiation, and Hanbury-Brown and Twiss (HBT) first investigated photon statistics in astronomical sources. Contemporary experiments combining thermal light and photon subtraction techniques have implemented effects such as ghost imaging, quantum illumination, and the "quantum" vampire effect, as well as tests of fundamental physics such as the bosonic commutation relation and Maxwell's demon.
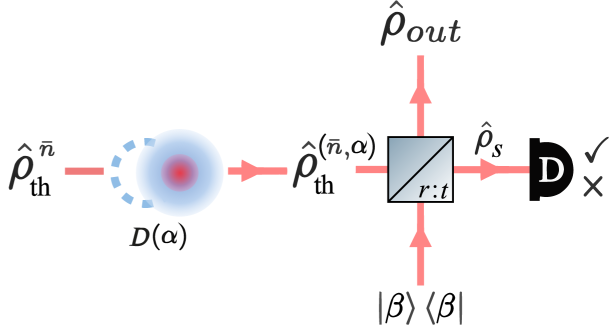
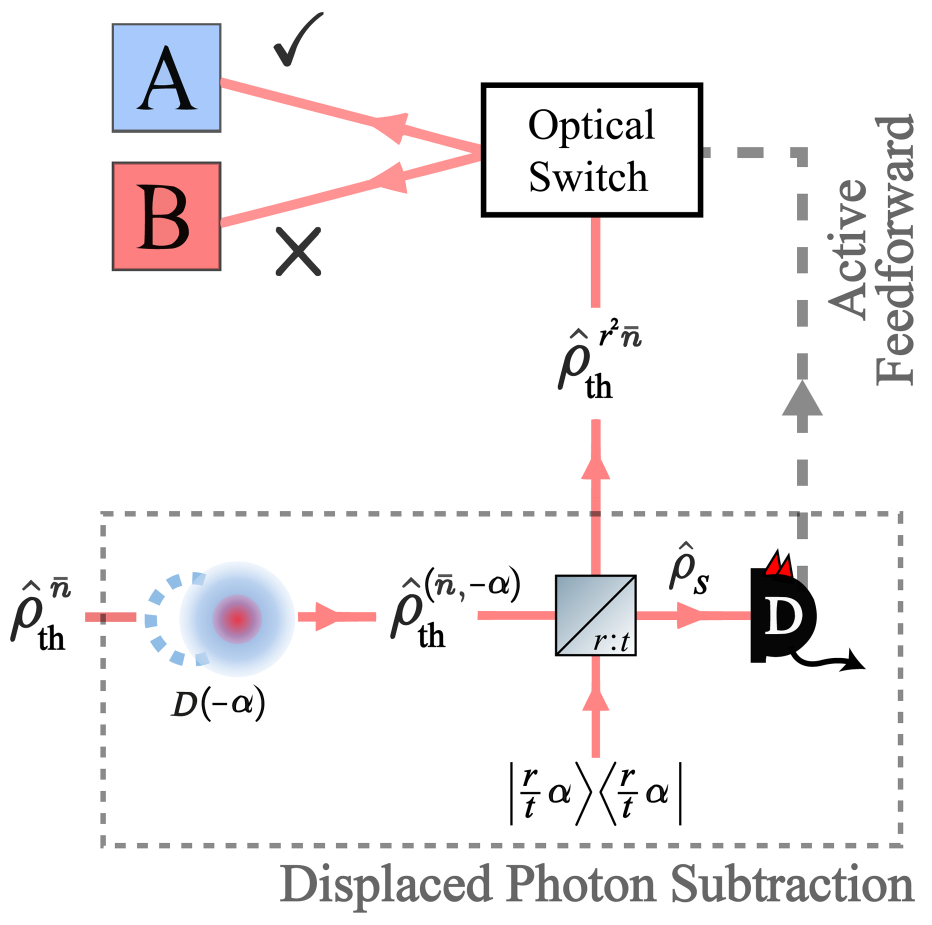
These applications often go hand in hand with photon subtraction operations which probabilistically amplify the mean photon number (MPN) of thermal light as a result of its super-Poissonian photon statistics. In this article, we introduce an operation for thermal states of light based on a generalized photon subtraction scheme. Displaced-photon subtraction (DPS) makes use of coherent state displacement followed by a subsequent anti-displacement in combination with single-photon detection to probe the MPN of a thermal state.
Differently, hypothesis testing, parameter estimation, and imaging are fundamental scientific tasks that can all be improved using quantum techniques. A judicious choice of quantum probe state or measurement observable can significantly improve the information gained in a measurement. These improvements can manifest in a multitude of ways. For example, the noise in an image may be reduced, or the resolution of the image may be improved beyond the classical Rayleigh limit.
Other improvements include ghost imaging, where information is extracted from quantum light that has not directly interacted with the object, and quantum-enhanced non-linear microscopy. Quantum lithography, and quantum sensing exploit entangled or correlated sources to enable precision beyond what is achievable classically. In microscopy, these techniques compete with classical super-resolution methods that use engineered sources that exhibit non-linear responses or exploit selective activation and bleaching of fluorophores.
When source engineering is not an option, which is the case for astronomical observations, quantum techniques can beat the diffraction limit by unlocking all the information about amplitude and phase in the collected light. However, prior to measuring the separation, one needs to ensure that there are two sources and not just one. One straightforward method would be to use direct imaging (DI) to determine whether a secondary source is present. In a diffraction limited system, the image of a point-like object is not a point but has a finite spread characterised by the point-spread function (PSF). If the two sources overlap on the image screen, this blurring presents a severe practical obstacle to direct detection of exoplanets, especially when one source is much dimmer than the other.
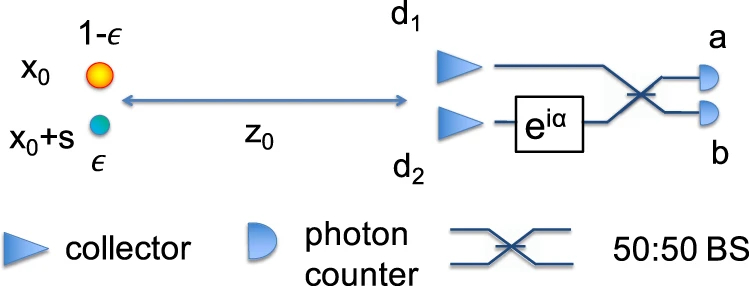
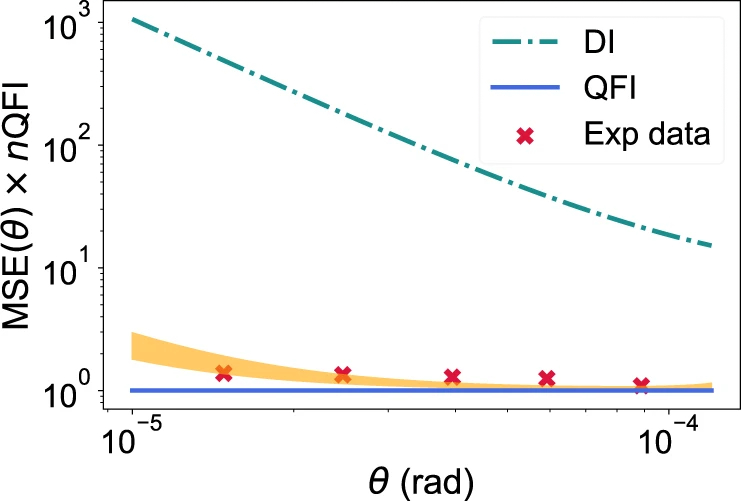
Quantum hypothesis testing techniques, on the other hand, can be used when the task is to determine whether a secondary source exists. The goal is to minimise the probability of a false negative (missing the second source). If we are happy to accept a certain probability of false positives (type-I error), then the probability of a false negative (type-II error) is given by the quantum Stein Lemma. This asymmetric error setting is particularly applicable to rare events such as exoplanet identification, or events with important ramifications such as dimer detection in microscopy.
Meet the researchers
Selected publications
- U. Zanforlin, G. Tatsi, J. Jeffers, and G. S. Buller, "Covert information sharing via ghost displacement", Physical Review A 107, Article Number 022619 (2023).
- G. Tatsi, D. W. Canning, U. Zanforlin, L. Mazzarella, J. Jeffers, and G. S. Buller, "Manipulating thermal light via displaced‑photon subtraction", Physical Review A 105, Article number 053701 (2022).
- Ugo Zanforlin, Cosmo Lupo, Peter W. R. Connolly, Pieter Kok, Gerald S. Buller and Zixin Huang, "Optical quantum super‑resolution imaging and hypothesis testing", Nature Communications 13, Article number 5373 (2022).